Р
|
Равенство комплексных чисел
|
Два комплексных числа 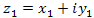 и и 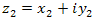 равны между собой, если попарно равны их вещественные и мнимые части: равны между собой, если попарно равны их вещественные и мнимые части:
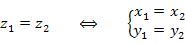
|
|
|
|
|
Разложение выражения на множители
|
Выражение “разложить на множители” означает “представить математическое выражение в виде произведения двух или большего числа множителей”.
Любой многочлен можно представить в виде произведения неприводимых многочленов, каждый из которых не допускает разложения на более простые множители. Для разложения многочлена на множители в некоторых случаях достаточно сгруппировать слагаемые и вынести общий множитель. В других случаях эта проблема успешно решается применением формул сокращенного умножения. Для разложения многочлена на множители можно также использовать процедуру выделения полного квадрата с последующим применением формулы разности квадратов. Если известен один из множителей многочлена, то оставшийся множитель можно найти, используя
|
|
|
|
|
Разложение на простые числа
|
Любое натуральное число можно представить в виде произведения простых чисел, каждое из которых не допускает разложения на иные множители - кроме единицы и самого числа. |
|
|
|
|
Разность множеств
|
Разностью A \ B называется множество элементов, каждый из которых содержится в A, но не содержится в B:
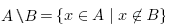
|
| Пример |
Если A = {1, 2, 3, 4, 5} и B = {2, 4, 6}, то
A \ B = {1, 3, 5},
B \ A = {6}. |
|
|
|
|
Рациональные числа
|
Любое рациональное число может быть представлено в виде отношения двух целых чисел, а также конечной десятичной дробью или бесконечной периодической дробью. Множество рациональных чисел 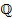 включает в себя подмножество целых чисел включает в себя подмножество целых чисел 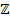 : :
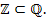
|
|
|
|