В
|
Вещественные числа
|
Множество вещественных чисел 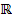 представляет собой объединение множества рациональных чисел представляет собой объединение множества рациональных чисел 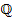 и множества иррациональных чисел и множества иррациональных чисел 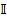 , что записывается а символическом виде как , что записывается а символическом виде как
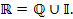
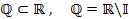
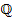 представляет собой подмножество множества вещественных чисел и является дополнением множества иррациональных чисел представляет собой подмножество множества вещественных чисел и является дополнением множества иррациональных чисел 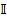 до множества до множества 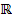 . .
|
|
|
|
|
Взаимно простые числа
|
Целые числа называются взаимно простыми, если они не имеют общих делителей, кроме ±1. Взаимно простые числа не обязательно должны быть простыми числами, однако, любые различные простые числа являются и взаимно простыми. |
| Пример |
Числа 21 и 22 являются взаимно простыми, тогда как числа 21 и 24 таковыми не являются, ибо у них имеется общий делитель 3. |
|
|
|
|
Виета теорема
|
Если приведённое квадратное уравнение 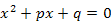 имеет два действительных различных корня, то сумма его корней равна второму коэффициенту, взятому с противоположным знаком, т. е. имеет два действительных различных корня, то сумма его корней равна второму коэффициенту, взятому с противоположным знаком, т. е. 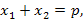 а произведение корней равно свободному члену, т. е. а произведение корней равно свободному члену, т. е. 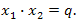
|
|
|
|
|
Возведение в степень
|
В выражении 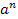 число a называется основанием, n – показателем степени, в которую возводится основание. число a называется основанием, n – показателем степени, в которую возводится основание.
Если n = 2 или n = 3, то выражения a2 и a3 называются соответственно квадратом и кубом числа a. |
|
|
|