. Возведем в квадрат обе части формулы Эйлера:
 .
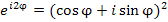Учитывая, что
получим
Равенство двух комплексных чисел влечет за собой попарное равенство их вещественных и мнимых частей. Следовательно,
|
***
|
. Аналогичным образом можно преобразовать тождество
основанное на формуле Эйлера:
Приравнивая попарно вещественные и мнимые части выражений в обеих частях этого равенства и учитывая основное тригонометрическое тождество
получим формулы тройного угла для синусов и косинусов:
|
***
. Используя формулу Эйлера, преобразуем произведение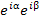 
Однако
Тогда
|
|
