SEARCH:
Нет данных.
Сегодня
25 апреля 2025 / Friday / Неделя четная
Time tableРасписание
  
    Мат. анализ, семестр 1     
    Мат. анализ, семестр 2     
    Мат. анализ, семестр 3     
    Лин. алг. и аналитич. геом.     

1. Функции одной переменной. Пределы последовательностей.
  1. Понятие последовательности. Бесконечно малые величины, их свойства.
  2. Бесконечно большие величины, их свойства.
  3. Предел последовательности, свойства пределов.
  4. Классификация бесконечно малых и бесконечно больших величин.
  5. Теоремы о пределах последовательностей.
  6. Число e. Второй замечательный предел.
  7. Бесконечно малые функции, их свойства.
  8. Предел функции, его геометрический смысл. Свойства пределов функций.
  9. Бесконечно большие функции. Сравнение бесконечно малых и бесконечно больших функций.
  10. Первый замечательный предел.
  11. Основные соотношения эквивалентности бесконечно малых (с обоснованием).
  12. Раскрытие неопределенностей различного вида.
  13. Односторонние пределы. Непрерывность функции в точке и на интервале.
  14. Классификация точек разрыва. Теоремы о непрерывных функциях.

2. Дифференцирование функции одной переменной.

  1. Задачи, приводящие к понятию производной функции. Производная функции. Физический и геометрический смысл производной. Правила дифференцирования функций.
  2. Таблица производных простейших элементарных функций.
  3. Дифференциал функции, его интерпретация. Свойства дифференциала, инвариантность формы первого дифференциала.
  4. Теоремы о дифференцировании обратной и сложной функций. Расширение таблицы производных функций.
  5. Применение дифференциала для приближенных вычислений. Логарифмическое дифференцирование. Дифференцирование неявно заданных функций и параметрически заданных функций.
  6. Касательная и нормаль к кривой, заданной в различных формах.
  7. Теорема Ферма.
  8. Теорема Ролля.
  9. Теорема Лагранжа.
  10. Теорема Коши.
  11. Производные и дифференциалы высших порядков. Формула Лейбница.
  12. Правило Лопиталя раскрытия неопределенностей вида 0/0.
  13. Правило Лопиталя раскрытия неопределенностей вида ∞/∞.
  14. Применение правила Лопиталя для раскрытия неопределенностей вида 1∞, ∞0, 00.
  15. Формула Тейлора для многочленов.
  16. Прелставление функций в виде разложений по Формуле Тейлора.
  17. Разложение функций ex , sinx , cosx , ln(1+x) , (1+x)m по формуле Тейлора.
  18. Применения формулы Тейлора.
  19. Исследование функции одной переменной. Симметрия функции. Возрастание и убывание функции на интервале. Точки экстремума. Необходимые и достаточные условия существования экстремума функции.
  20. Наименьшее и наибольшее значения функции на отрезке.
  21. Интервалы выпуклости и вогнутости кривой, точки перегиба. Необходимые и достаточное условия существования точки перегиба.
  22. Асимптоты функции. Полное исследование функции и построение графиков.
  23. Геометрические и физические приложения экстремумов функций.

3. Функции нескольких независимых переменных.

  1. Обобщение основных понятий анализа на случай функций нескольких независимых переменных. Область определения функции нескольких переменных. Предел и непрерывность функции нескольких переменных.
  2. Частные производные, их геометрический смысл.
  3. Дифференциал функции нескольких переменных. Производная сложной функции.
  4. Полная и частная производные.
  5. Неявные функции и их дифференцирование.
  6. Производные и дифференциалы высших порядков. Инвариантность формы первого дифференциала. Применение дифференциала для приближенных вычислений.
  7. Геометрический смысл функции двух переменных. Касательная плоскость и нормаль к поверхности.
  8. Экстремум функции двух переменных, необходимые и достаточные условия. Седловые точки.
  9. Наибольшее и наименьшее значения функции двух переменных в замкнутой области.
Банк задач по теме "Пределы последовательностей и функций".
Задачи по теме "Неопределенные интегралы".
Банк задач, из числа которых формируются экзаменационные задания (число задач: 118). 
Образцы экзаменационных билетов по математическому анализу. Первый семестр 2009-2100 уч. года. 1-ый курс ЭТО.

Электронный учебник: Пределы последовательностей и функций, производные и дифференциалы, неопределенные и определенные интегралы, ... 
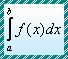Избранные разделы математического анализа.Избранные разделы математического анализа.
Учебное пособие основано на курсе лекций, читаемых автором для студентов отделения элитного технического образования ТПУ, и включает в себя следующие разделы: – Формула Тейлора – Функции нескольких переменных – Неопределенные интегралы – Определенные интегралы – Несобственные интегралы Наряду с изложением теоретического курса в пособии содержится большое число примеров и графических иллюстраций. 
2011 © Томский политехнический университет
При полном или частичном использовании текстовых и графических материалов с сайта ссылка на портал ТПУ обязательна