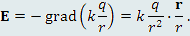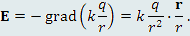-
-
Какой смысл имеет величина градиента скалярного поля?
-
Как можно формально обосновать справедливость приведенного утверждения?
-
Постарайтесь привести пример скалярного поля, градиент которого равен нулю. Какой физический смысл имеет такое поле?
-
-
Чему равна производная суммы?
-
Чему равна производная от константы?
-
-
Воспользуйтесь правилом дифференцирования суммы двух функций и перегруппируйте слагаемые.
-
-
Чему равна производная от произведения двух функций?
-
Воспользуйтесь правилом дифференцирования произведения двух функций и перегруппируйте слагаемые.
-
-
Радиус-вектором точки
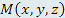 является вектор r = i x + j y + k z, проведенный из начала координат в эту точку. является вектор r = i x + j y + k z, проведенный из начала координат в эту точку.
-
Запишите выражение для величины радиус-вектора r.
-
Является ли правильным утверждение, что
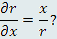
-
Чему равны частные производные от r по переменным y и z?
Ответ: 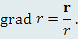
-
-
Чему равен скалярный квадрат радиус-вектора r?
-
Является ли правильным утверждение, что
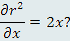
Ответ: 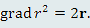
-
-
Найдите градиент скалярного поля φ в произвольной точке.
-
Вычислите градиент в заданной точке.
-
Найдите модуль полученного вектора.
-
-
В какой точке следует выбрать начало прямоугольной системы координат, чтобы расстояние от произвольной точки до заряда совпадало с величиной радиус-вектора этой точки?
-
Как найти градиент функции
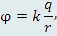 учитывая, что kq является постоянным множителем? учитывая, что kq является постоянным множителем?
Ответ: 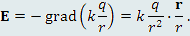
|
-
Доказать, что
где C – константа.
-
Доказать, что
если C – константа.
-
Доказать, что
-
Доказать, что
-
Вычислить градиент скалярного поля φ = r, где r – величина радиус-вектора произвольной точки
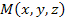 . .
-
Вычислить градиент скалярного поля
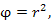 где r – величина радиус-вектора произвольной точки где r – величина радиус-вектора произвольной точки 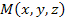 . .
-
Вычислить градиент скалярного поля
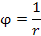 в точке в точке 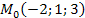 и быстроту изменения функции φ в этой точке. и быстроту изменения функции φ в этой точке.
-
Потенциал φ точечного заряда q описывается формулой
где r – расстояние от заряда; k – константа.
Найти напряженность электрического поля 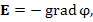 создаваемого этим точечным зарядом. создаваемого этим точечным зарядом.
Справка по теме:
Линии и поверхности уровня скалярного поля.
|
Линии и поверхности уровня скалярного поля
Геометрическое место точек, в которых скалярное поле принимает одно и то же значение.
Поверхности уровня скалярного поля φ описываются уравнением
φ (x, y, z) = C.
|
Справка по теме:
Векторные линии поля.
|
Векторные линии поля
представляют собой кривые, касательные к которым в любой точке указываают направление поля в этой точке.
|
|