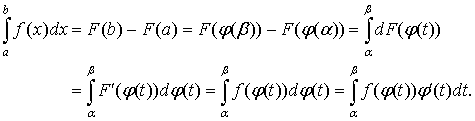| Definition and Properties |
The Geometric Definition of Definite Integrals
The Algebraic Definition of Definite Integrals
Properties of Definite Integrals
| Fundamental Theorems of Calculus |
The First Fundamental Theorem of Calculus
The Second Fundamental Theorem of Calculus
| Techniques of Integration |
Substitution Method
Integration by Parts
| Techniques of Integration: Substitution Method |
| Key Topics Remaining: Integration by Parts |
|
Let f (x)
be a continuous function on the interval [a,
b]. Proof. Let f (x) be a primitive of f (x) on the interval [a, b]. Applying Fundamental Theorem 2 of calculus and in view of the properties of primitives, we have |
Note that it is not necessary to come back to the initial variable.
|
|
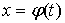 has a continuous derivative on the interval
has a continuous derivative on the interval 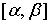 .
.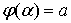 and
and 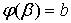 , then
, then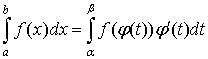 .
.