| Definition and Properties |
The Geometric Definition of Definite Integrals
The Algebraic Definition of Definite Integrals
Properties of Definite Integrals
| Fundamental Theorems of Calculus |
The First Fundamental Theorem of Calculus
The Second Fundamental Theorem of Calculus
| Techniques of Integration |
Substitution Method
Integration by Parts
| Properties of Definite Integrals |
| Key Topics Remaining: The First Fundamental Theorem of Calculus » The Second Fundamental Theorem of Calculus » Substitution Method » Integration by Parts |
- The variable of integration is a dummy variable, that is, an integral is independent of a symbol denoting the variable of integration,
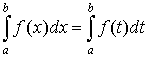 .
.
- If c is a constant then
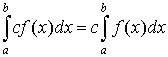 .
.
- If there exist integrals of f (x) and g (x) over the interval [a, b] then
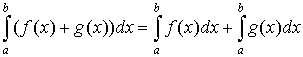 .
.
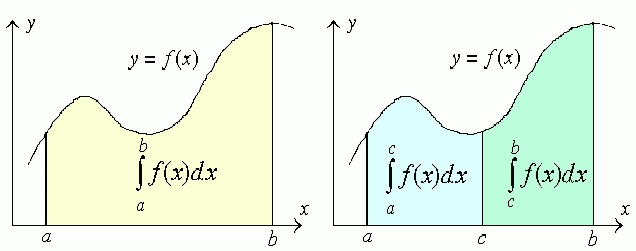
Property 7 in a case of a
< c < b.
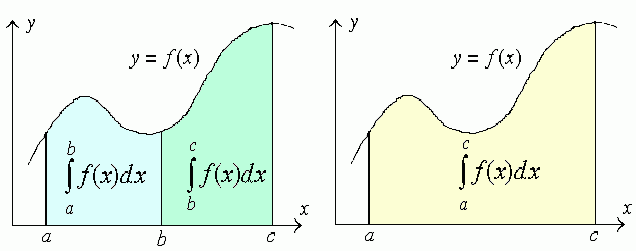
Property 7 in a case of a
< b < c.
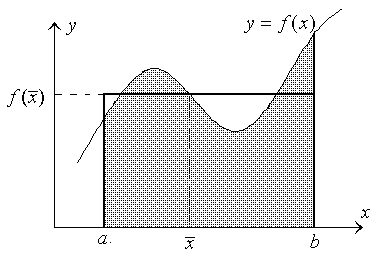
The area of the figure under the curve y
= f (x)
equals the area of the rectangular
with the base b – a and
the height f (x).
|
|
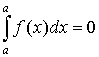 .
.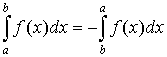 .
.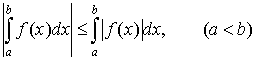 .
.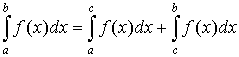 .
.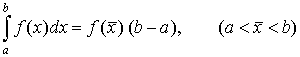 .
.