| Definition and Properties |
The Geometric Definition of Definite Integrals
The Algebraic Definition of Definite Integrals
Properties of Definite Integrals
| Fundamental Theorems of Calculus |
The First Fundamental Theorem of Calculus
The Second Fundamental Theorem of Calculus
| Techniques of Integration |
Substitution Method
Integration by Parts
| Algebraic Definition of Definite Integrals |
| Key Topics Remaining: Properties » The First Fundamental Theorem of Calculus » The Second Fundamental Theorem of Calculus » Substitution Method » Integration by Parts |
Let f (x) be a function defined on a closed interval [a, b]. Consider a partition of the interval [a, b] taking points x1, x2, …, xn-1 such that
![]() .
.
The sum of the products f (xk)
Δxk is
the Riemann Sum, where Δxk denotes the difference between
two successive partition points, ![]() .
.
Let ![]() and all
and all ![]() .
.
If the limit of a sequence of the Riemann Sums exists and does not depend on partition points xk , then this limit is called a definite integral of the function f (x) over the interval [a, b],
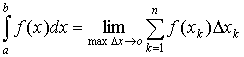 .
.
The evaluation of definite integrals is called the integration.
|
|