Mathematical Induction Principle

Discrete Algebra

Binomial Theorem

Sigma-Notations

Arithmetic Progressions

Geometric Progressions

Binomial Theorem

Pascal's Triangle

Evaluation of Sums of the Form
1k + 2k + ... + nk

1 + 2 + ... + n

1² + 2² + ... + n²

1³ + 2³ + ... + n³

Mathematical Induction Principle

Basic Conceptions

Constituents of the Induction Principle

Model Examples
Example 1
Example 2
Example 3
Example 4
Example 5
Example 6

Mathematical Induction Principle:
Example 5

Key Topics Remaining: Example 6

Problem. Prove that if q ≠ 1 then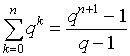

Proof. Let Pn be the proofable statement.
One can easily check up that the satement P0 is true.

Assume that Pn is also true for some integer n > 0.
Then

Since the statement Pn implies Pn+1 , the formula is proved.