INDEX
Numbers and Sets
Complex Numbers
Exponentiation
Algebraic Transformations
Algebraic Equations and Inequalities
Functions
Basic Formulas
Graphics of Basic Functions
Discrete Algebra
Ship 2

Binomial Theorem

Sigma-Notations

Arithmetic Progressions

Geometric Progressions

Binomial Theorem

Pascal's Triangle

Evaluation of Sums of the Form
1k + 2k + ... + nk

1 + 2 + ... + n

1² + 2² + ... + n²

1³ + 2³ + ... + n³

Mathematical Induction Principle

Basic Conceptions

Constituents of the Induction Principle

Model Examples
  Example 1
  Example 2
  Example 3
  Example 4
  Example 5
  Example 6

Mathematical Induction Principle:
Example 4
Key Topics Remaining:   Examples  5,   6, 

Problem.  Prove that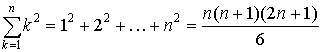

Proof.  Let  Pn  be the proofable statement.

  1. Induction basis:  The statement  P1  means that
    .
    That is true.

  2. Induction hypothesis: Assume that the proofable equality holds true for some integer  n > 1.

  3. Induction step: We have to prove that the truth of  Pn  implies the validity of  Pn+1, that is,

    .

Really,

Hense, the equality.
Previous Topic   Next Topic