
 |
| Discrete Algebra |

Sigma-Notations Arithmetic Progressions Geometric Progressions Binomial Theorem Pascal's Triangle
1 + 2 + ... + n 1² + 2² + ... + n² 1³ + 2³ + ... + n³
Basic Conceptions Constituents of the Induction Principle Model Examples Example 1 Example 2 Example 3 Example 4 Example 5 Example 6 |
Binomial coefficients are defined by the following formula, 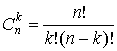 . .The symbol n! is read "n factorial" that means the product of all natural numbers from 1 to n: n! = 1·2·3·…·n.
By definition, 0! = 1.
The binomial coefficients give a number of choices of
k objects from a set of n
objects, regardless of the order in which the objects are chosen.
If a = 1 and b = x then 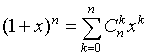 . .The binomial coefficients can also be found by making use of the Pascal's triangle.
|