| |
|
|
|
|
|
|
|
|
|
|
| Algebraic Equations and Inequalities |
 Properties of Equations and Inequalities Graphical Interpretation of Solutions
Linear Equations Linear Inequalities
Linear Equations Involving Absolute Value Linear Equations Involving a Few Absolute Values Linear Inequalities Involving Absolute Value
 Quadratic
EquationsQuadratic Equations and Quadratic Functions Extreme Value of Quadratic Function Quadratic Formula Solving Quadratic Equations by Factoring Quadratic
Inequalities |
|
|
In order to solve a quadratic equation, a x2 + b x + c = 0, rewrite it by completing the perfect square: 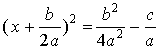 Reduce the right side to the common denominator:  The value D = b2
– 4 a c is called the discriminant
of the quadratic equation. The sign of the discriminant is an important
characteristic of a quadratic equation. 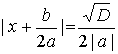 ,which implies the quadratic formula,
In a particular case when a = 1 and b is an even number, the quadratic formula has a more convenient form,  .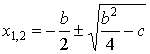
|
.
.
