Inequalities involving the absolute value  | a x + b |  can be solved by applying just the same technique as in case of equations.
First of all, it is necessary to find the point, in which the expression  a x + b  changes its sign.
Then we have to consider two cases,  a x + b ≥ 0 and  a x + b < 0, to reduce the given problem to solving usual linear inequalities, satisfying the corresponding conditions.

The solution set for the given inequality is the union of the solutions obtained in both cases.

Sometimes, one can easily write down the solution set, using the following properties of absolute values: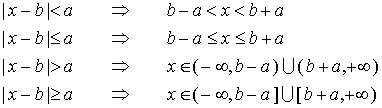

Index Real Numbers Complex Numbers Exponentiation Algebraic Transformations Algebraic Equations and Ineualities Functions Discrete Algebra Basic Formulas Graphics of Basic Functions