| |
|
|
|
|
|
|
|
|
|
|
| Algebraic Equations and Inequalities |
 Properties of Equations and Inequalities Graphical Interpretation of Solutions
Linear Equations Linear Inequalities
Linear Equations Involving Absolute Value Linear Equations Involving a Few Absolute Values Linear Inequalities Involving Absolute Value
 Quadratic
EquationsQuadratic Equations and Quadratic Functions Extreme Value of Quadratic Function Quadratic Formula Solving Quadratic Equations by Factoring Quadratic
Inequalities |
|
|
In order to solve graphically an equation f ( x ) = 0, it is necessary to find the points at which a curvey = f ( x ) intersects or touches the x-axis.
In order to find the x-intercepts of the
function y = f (x),
set y = 0 and solve
the equation f (x) = 0 for
x.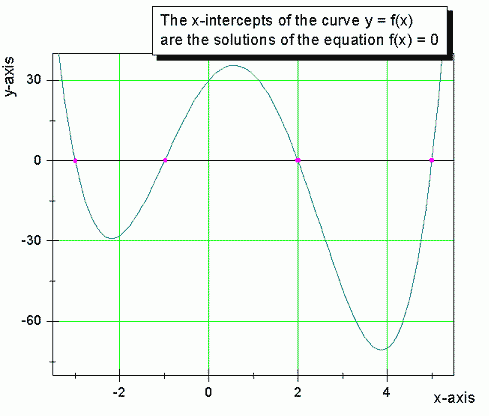 
|
