Solutions of a quadratic equation can be interpreted in terms of  x-intercepts of a quadratic function,

y = a x2 + b x + c,

a graph of which is a parabola, that is, a curve consisting of two symmetric branches (as it is shown in the figures below).

The number of the  x-intercepts depends on the position of the vertex of the parabola, that is, the number of roots of a quadratic equation depends on relationships between coefficients.

By completing the perfect square, the quadratic function can be transformed to the form

where    and    are coordinates of the vertex of the parabola.

1. If  y0  > 0,  then the vertex of the parabola lies above the x-axis, and so the quadratic equation,
   a x2 + b x + c = 0,
   has not any real roots.
2. If  y0 = 0,  then the vertex of the parabola touches on the x-axis at the point  x = x0,  and therefore, the quadratic equation has one real root, x = x0.
3. If  y0 < 0,  then the vertex of the parabola lies under the  x-axis, and each of two branches of the parabola intersects the x-axis. Therefore, the quadratic equation has two real roots.

There exist simple relationships between the roots  (x1 and x2)  of the quadratic equation and the coordinates  (x0 and y0)  of the vertex of the parabola: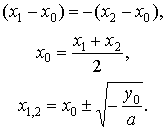

Index Real Numbers Complex Numbers Exponentiation Algebraic Transformations Algebraic Equations and Ineualities Functions Discrete Algebra Basic Formulas Graphics of Basic Functions