| |
|
|
|
|
|
|
|
|
|
|
| Algebraic Equations and Inequalities |
 Properties of Equations and Inequalities Graphical Interpretation of Solutions
Linear Equations Linear Inequalities
Linear Equations Involving Absolute Value Linear Equations Involving a Few Absolute Values Linear Inequalities Involving Absolute Value
Quadratic Equations Quadratic Equations and Quadratic Functions Extreme Value of Quadratic Function Quadratic Formula Solving Quadratic Equations by Factoring  Quadratic
Inequalities |
|
|
The general form of a quadratic equation is a x2
+ b x + c = 0,
where x is the variable; a,
b, and c are constants Since the expression on the left-hand side is a polynomial
of the second degree, the above equation is also called a second-degree
equation.
It can also be rewritten in form of a monic quadratic equation, if to divide the both sides by the coefficient a:
An equation of the form, a x2
+ c = 0,
is called an incomplete quadratic.
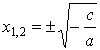 A quadratic equation of a common form can be solved by
|
.
