
Cartesian Coordinate System

Domain and Range

Inverse Functions

Even-Odd Symmetry of Functions

Periodicity of Functions
| Exponential and Logarithmic Functions |

Exponential Functions

Logarithmic Functions
Natural Logarithms

Hyperbolic Functions
|

|

|
E are functions of the
form
y = ax
where the base a is a positive number and a ≠ 1.
The of an exponential function is the
set of real numbers.
The of an exponential function is the
set of positive real numbers.
Exponential functions have the following .
- ax
> 0 for any real numbers x.
- ax
= az
if and only if x = z.
- If a > 1 then exponential
functions are monotone increasing functions and so ax
> az
for x > z.
- If 0 < a < 1 then exponential
functions are monotone decreasing functions and so ax
< az
for x > z.
- If a > 1 and x
→ + ∞ then ax
→ + ∞.
If a > 1 and x
→ – ∞ then ax
→ 0.
- If 0 < a < 1 and
x → + ∞
then ax
→ 0.
If 0 < a < 1 and x
→ – ∞ then ax
→ + ∞.
- A graph of any exponential function lies above the x-axis
and includes the point ( 0, 1 ).
- Graphs of functions y = ax
and y = a–
x are mirror reflections of each other with respect
to the y-axis.
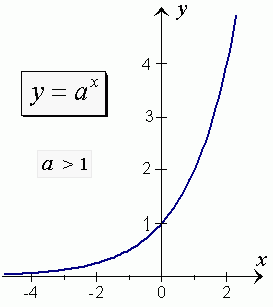 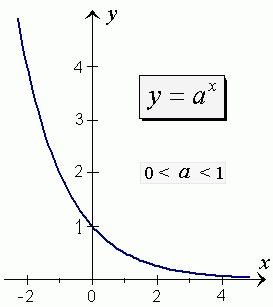
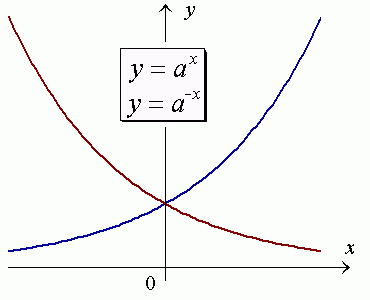
Transformations of exponential functions are based on Exponential
Identities.
|


