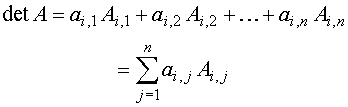| Theorem |
|
A determinant of a matrix A equals the sum of the products of elements of any row of A and the corresponding cofactors: |
Proof: By the definition,
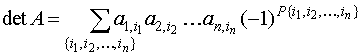 .
.
We can combine similar terms to represent the above sum in the form
![]() ,
,
where
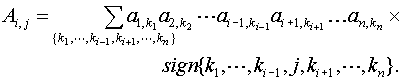
Note that
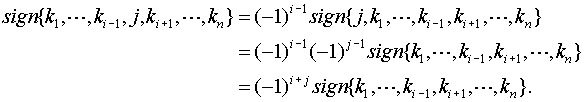
Therefore,
![]() .
.
In this formula
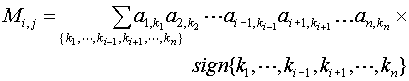
is the minor of the element ai,j.
Thus, Ai,j is the cofactor of the element ai,j.