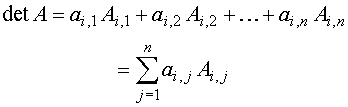|
1. Expanding a determinant by a row or column |
Before formulating the theorem, let us introduce a few definitions.
Let A be a square matrix of the order n. By removing the i-th row and the j-th column, we obtain the submatrix of A, having the order n - 1.
The determinant of that submatrix is called the minor of the element ai,j, which is denoted by Mi,j:

The cofactor of the element ai,j
is defined as the minor Mi,j
with the sign ![]() . It is denoted by the symbol Ai,j:
. It is denoted by the symbol Ai,j:
![]() .
.
The following theorem gives a systematic procedure of determinant calculation.
| Theorem |
|
The determinant of a matrix A equals the sum of the products of elements of any row of A and the corresponding cofactors: |
The above theorem is known as the expansion of the determinant according to its i-th row.
Since a matrix and its transpose have equal determinants, the theorem can be formulated in terms of expanding of a determinant by a column:
|
The determinant of a matrix A equals the sum of the products of elements of any column of A and the corresponding cofactors: |
Due to the theorem, a given determinant of the order n is reduced to n determinant of the order (n - 1).
|
2. Evaluation of determinants by elementary operations on matrices |
By means of elementary row and column operations on matrices, a determinant can be transformed to a triangular form, which is easily evaluated.
Let us define the elementary operations. Note that any techniques which are developed for rows may be also applied to columns.
Elementary Operations:
- Interchange two rows or columns.
As a result, the determinant changes its sign. - Multiply a row (column) by a nonzero number.
As a consequence of this operation, the determinant is multiplied by that number. - Add a row (column) multiplied by a number
to another one.
By this operation, the determinant holds its value.