Let be a square matrix of the order n, and let be the ordered set of the first n natural numbers.

Consider the following product of n matrix elements:

(1)

where is a permutation of S, and is the inversion parity of the permutation . That is, for an even permutation, and for an odd one:

.

Note that is an element on the first row and k1-th column, is on the second row and k2-th column, and so on.

Therefore, expression (1) is the product of matrix elements such that each row and each column of A is presented by one and only one its element. According to Theorem 2, there are n! different permutation of S, and each permutation generates the product of such type as (1).

The sum of all possible products (1) over permutations is called the determinant of matrix A and denoted by the array between vertical bars:

Thus,

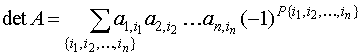The above sum contains n! items, fifty-fifty with even and odd permutations.

Do not forget that a numerical matrix is rectangular table of numbers while the determinant of a matrix is just one number, which is an important characteristic of the matrix.

Some particular cases

1. The determinant of a matrix of the first order is the element itself.

2. The determinant of a matrix of the second order

Let A be a square matrix of the second order:

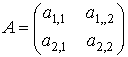
There are possible only two permutations of {1,2}: {1,2} and {2,1}.

The permutation {1,2} is even, since it has no inversions, while the permutation {2,1} has one inversion of the elements and so is odd.

These permutations generate two products:

and

.

Therefore,

.

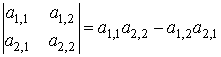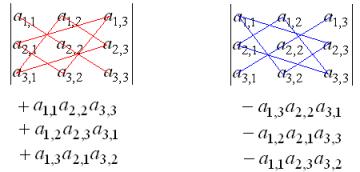
3. The determinant of a matrix of the third order

There are possible six permutations of the set {1, 2, 3}:

{1, 2, 3}, {2, 3, 1}, {3, 1, 2},

{3, 2, 1}, {2, 1, 3}, {1, 3, 2}.

The permutations {1, 2, 3}, {2, 3, 1} and {3, 1, 2} are even since they have even numbers of inversions of elements.

The permutations {3, 2, 1}, {2, 1, 3} and {1, 3, 2} are odd since they have odd numbers of inversions of elements. [See details in Examples.]

Therefore,

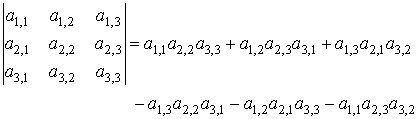
To remember this formula for determinants of the third order, apply the Sarrus Rule that is represented in the drawing below.