Evaluate the determinant of the matrix

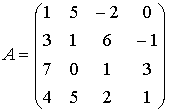
Solution: First, transform the first row via elementary column operations. Keeping the first and last columns, subtract the first column multiplied by 5 from the second one, and add the first column multiplied by 2 to the third one:

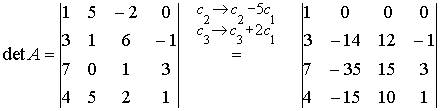
Then apply the theorem of expanding a determinant by the first row:

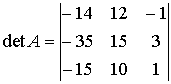
Transform the third column by adding the third row to the first one and subtracting the third row multiplied by 3 from the second row:

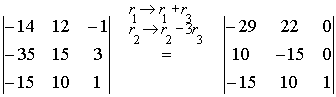
Expand the determinant by the third column:

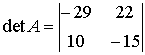
We can still take outside the common factor 5 from the last row:

.
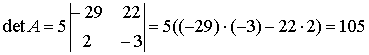