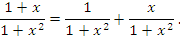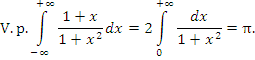Рассмотрим несобственный интеграл по бесконечному промежутку  , не содержащий особенностей внутри этого промежутка. По определению , не содержащий особенностей внутри этого промежутка. По определению
 и и 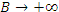 выполняются независимо один от другого. выполняются независимо один от другого.
Если такой двойной предел не существует, но существует предел, когда A и B удовлетворяют требованию A = –B, то этот предел называется главным значением несобственного интеграла 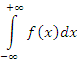 : :
|
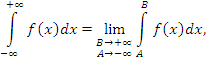
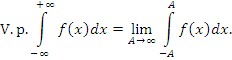
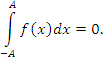
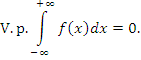
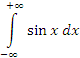 не существует, тогда как соответствующий интеграл в смысле главного значения равен нулю:
не существует, тогда как соответствующий интеграл в смысле главного значения равен нулю:
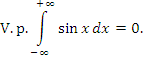
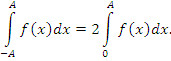
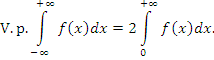
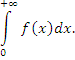 .
.
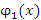 и нечетной
и нечетной 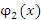 функций:
функций:
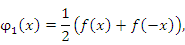
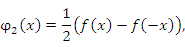
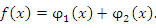
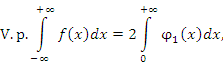
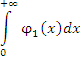 .
.
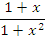 может быть представлена в виде следующей суммы четной и нечетной функций:
может быть представлена в виде следующей суммы четной и нечетной функций: