|
Рассмотрим задачу о нахождении кривой y = y0(x), на которой функционал
| |
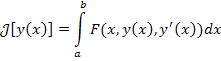
|
(1) |
|
достигает своего наибольшего или наименьшего значения. Решение будем искать в классе функций с фиксированными граничными точками.
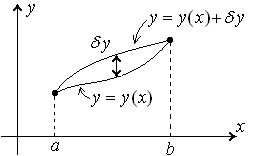
Согласно формуле (6) необходимое условие экстремума функционалов рассматриваемого типа имеет вид
| |
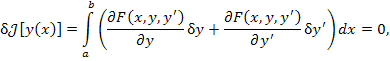
|
(2) |
|
где δy – вариация функции y = y (x), представляющая
собой дифференцируемую функцию переменной x;
δy' – вариация производной функции y = y (x).
Отметим, что δy' = (δy)'.
Проинтегрируем по частям второе слагаемое, выбрав
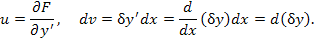
Тогда
| |

|
(3) |
|
Поскольку вариации функции в граничных точках равны нулю, то условие экстремума функционала принимает вид
| |
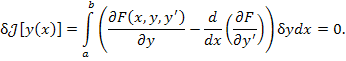
|
(4) |
|
Равенство нулю интеграла от произведения двух функций, одной из которых является произвольная функция
δy(x), влечет за собой обращение в нуль оставшегося сомножителя. (Это утверждение выражает суть
основной леммы вариационного исчисления. Чтобы ознакомиться с идеей ее доказательства, щелкните
указателем курсора по этой ссылке.)
Следовательно,
| |
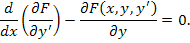
|
(5) |
|
Полученное уравнение называется уравнением Эйлера, роль которого в вариационном исчислении трудно переоценить.
|