Основная лемма   
       Пусть  f (x)  – непрерывная на отрезке  [a, b]  функция и при этом
   (1)  
для любой непрерывной функции  η(x).
       Тогда  f (x) = 0  на промежутке  [a, b].

       Доказательство. Предположим, что на промежутке  [a, b]  существует точка  x0, в которой функция  f (x)  отлична от нуля и принимает, например, положительное значение. Тогда в силу непрерывности функции она сохраняет свой знак и в некоторой  δ-окрестности этой точки.

       Выберем в качестве функции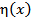    такую функцию, которая принимает положительные значения в указанной  δ-окрестности точки  x0  и равна нулю всюду за ее пределами:

Тогда подынтегральная функция является положительно определенной на промежутке интегрирования и, следовательно,

       что противоречит условию леммы.
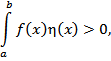
       Интуитивное восприятие этой леммы иллюстрируется представленной ниже анимацией.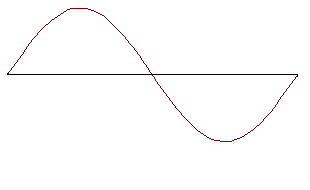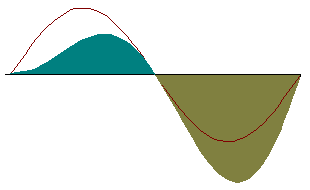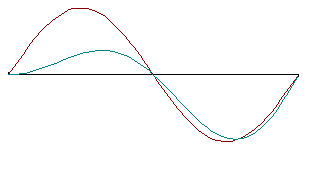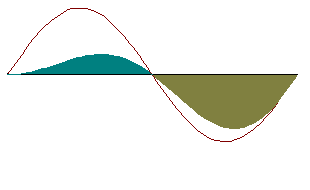

       Площадь области, расположенной выше оси  0x, вносит положительный вклад в соответствующий определенный интеграл, тогда как вклад области, расположенной ниже этой координатной линии, является отрицательным. Равенство нулю интеграла достигается только за счет взаимной компенсации положительной и отрицательной составляющих.
       Если изменить один из сомножителей подынтегрального выражения, то такой баланс может нарушиться и для равенство нулю интеграла необходимо, чтобы другой сомножитель был тождественно равен нулю на промежутке интегрирования.