To simplify a fraction means, in particular, to eliminate terms involving radicals from the denominator of the fraction. This procedure is known as rationalizing the denominator.
As a rule, a denominator can be rationalized by simple algebraic transformations.
The main idea is quite clear. To rationalize a denominator, it is necessary to find a factor that by which the given denominator is multiplied to produce an expression or quantity without radicals.
Let us consider a few typical cases.

1. If a denominator contains the square root of some expression as a factor, then multiply the numerator and denominator by the square root of the expression.
   
   Examples:

   

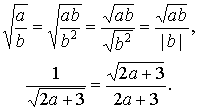
2. If a denominator involves a binomial expression like , then in view of the formula for the difference between two squares,

   .

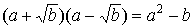   Therefore, one can multiply the numerator and denominator by 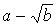to rationalize the denominator:

   .

   Likewise,

   

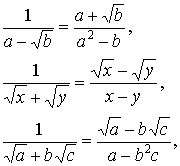
   and so on.

3. Let the denominator be a trinomial expression such as

   
   or something similar.
   Taking into account the formula for the difference between two cubes, we can use the factor 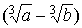to eliminate the denominator from radicals:

   

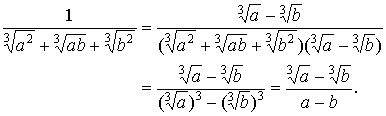
   Likewise,

   

Index Real Numbers Complex Numbers Exponentiation Algebraic Transformations Algebraic Equations and Ineualities Functions Discrete Algebra Basic Formulas Graphics of Basic Functions