Expanding is the inverse transformation of factoring.
We need to perform expanding an expression (or some parts of an expression) in order to simplify the expression or reformulate a problem. In particular, many integrals are evaluated by expanding the integrands.

Let us consider a few examples.

1. If to remove the parentheses in the expression  (a - b)( a + b), then we obtain once again the formula for the difference between two squares:

    (a - b)( a + b) = a2 – b2.

2. Expanding the expression  (a + b) (a2 – a b + b2), we come back to the formula for the sum of two cubes:

   (a + b) (a2 – a b + b2) = a3 + b3.

3. Likewise,

   (a – b) (a2 + a b + b2) = a3 – b3,
   (a ± b)2 = (a2 ± 2 a b + b2),
   (a + b)3 = (a3 + 3 a2 b + 3 a b2 + b3).

4. If we represent the below expressions in expanded form and compare the results with the original forms, then no explanation required.

   

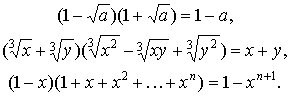
Index Real Numbers Complex Numbers Exponentiation Algebraic Transformations Algebraic Equations and Ineualities Functions Discrete Algebra Basic Formulas Graphics of Basic Functions