| Properties Involving Multiplication |
 |
Properties 1, 2 follow from the properties of real numbers.
Property 3 follows from the definition of a zero-matrix.
Property 4
Let A, B, and C be three matrices such that all multiplications are appropriate. Then
(AB)C = A(BC).
Proof: We have to show that the corresponding elements of matrices (AB)C and A(BC) are equal.
By the definition, the element on the i-th row and the k-th column of the product AB is
.
Then the element on the i-th row and the j-th column of the product (AB)C is
.
Changing the order of summation, we obtain
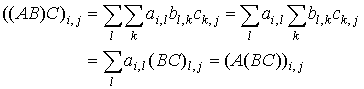
The equality of the corresponding matrix elements implies the equality of the matrices.
Property 5
Let A and B be two matrices such that the product AB is defined. Then
.
Proof: Consider the element on the i-th row and the j-th column of the matrix
:
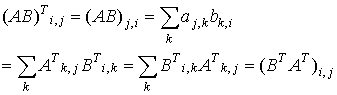
Thus, each element of 
is equal to the corresponding element
of 
, that means the equality of the
matrices.
Property 6
Let A be a 
matrix and let E
be the identity matrix of the n-th order.
Then
AE = A.
Proof: We need to show that each element of AE is equal to the corresponding element of A.
Consider the element on the i-th row and the j-th column of the matrix AE.
By the property of the Kronecker delta symbol, we have
for each pair of indexes {i, j}.
Hence, the desired statement AE = A.
If A is a square matrix then we can also perform the product EA:
.
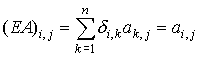| Properties Involving Addition and Multiplication |
|
Property 1
Let A, B, and C be three matrices such that the corresponding products and sums are defined. Then
A(B + C) = AB + AC
and
(A + B)C = AC + BC.
Proof: Consider the element on the i-th row and the j-th column of the matrix
. By the definition of the product
of matrices and in view of the addition properties, we have
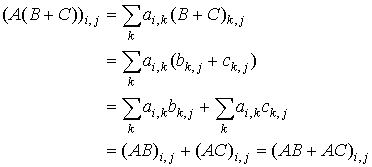
for each pair of indexes {i, j}.
Therefore, the matrices A(B + C) and (AB + AC) are equal.
The equality of the matrices (A + B)C and (AC + BC) can be proven just in the same way:
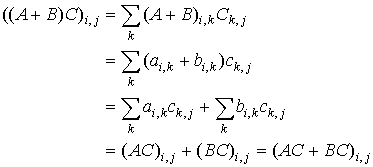
Property 2 follows from the properties of real numbers. The proof can be performed by the reader.
