| Properties Involving Addition |
- For any matrix A there exists the opposite matrix (-A) such that the sum
A + (- A) = A - A = 0
is a zero-matrix.
- If two matrices, A and B, have the same size then
A + B = B + A.
- If three matrices, A, B, and C, have the same size then
(A + B) + C = A + (B + C).
- The transpose of the sum of matrices is the sum of transpose of the matrices:
![]() .
.
All Addition Properties follow from the properties of real numbers. The proofs are left to the reader.
| Properties Involving Multiplication |
- Let A be a matrix, and let
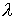 and
and 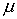 be numbers. Then
be numbers. Then
![]() .
.
- Let
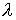 be a number and let A
and B be two matrices such that the product
AB is defined. Then
be a number and let A
and B be two matrices such that the product
AB is defined. Then
![]() .
.
- The product of a
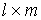 matrix A
and the
matrix A
and the 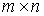 zero-matrix 0
is the
zero-matrix 0
is the 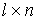 zero-matrix:
zero-matrix:
![]() .
.
- Let A, B, and C be three matrices such that all multiplications are appropriate. Then
(AB)C = A(BC).
- Let A and B be two matrices such that the product AB is defined. Then
![]() .
.
- Let A be a
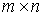 matrix and let E
be the identity matrix of the n-th order.
Then
matrix and let E
be the identity matrix of the n-th order.
Then
AE = A.
In a special case when A is a square matrix:
AE = EA =A.
| Properties Involving Addition and Multiplication |
- Let A, B, and C be three matrices such that the corresponding products and sums are defined. Then
A(B + C) = AB + AC
and
(A + B)C = AC + BC.
- Let
 be a number and let A
and B be two matrices of the same size.
Then
be a number and let A
and B be two matrices of the same size.
Then
![]() .
.
Note: By the definitions and properties of matrices, a number is a particular case of a matrix of the first order. Therefore, a set of real numerical matrices is a generalization of the set of real numbers.