С   
Связанные состояния
Состояние системы частиц, при котором относительное движение частиц происходит в ограниченной области пространства (является финитным) в течение длительного времени по сравнению с характерными для данной системы периодами.

Для образования связанных состояний необходимо наличие сил притяжения по крайней мере между некоторыми частицами системы на некоторых расстояниях между ними.
В квантовой механике, в отличие от классической, для образования связанных состояний частиц необходимо, чтобы потенциальная энергия притяжения и радиус действия сил были достаточно велики.
На рисунке показана зависимость потенциальной энергии U от расстояния r между частицами.

Стабильным связанным состояниям соответствуют дискретные уровни энергии системы.
Сегнетополупроводники
Кристаллы, обладающие одновременно сегнетоэлектрическими и полупроводниковыми свойствами.
В сегнетополупроводниках при определённых температурах и в отсутствие внешнего электрического поля существует спонтанная электрическая поляризация (электрический дипольный момент), которая может существенным образом изменяться под влиянием внешних воздействий (внешнее электрическое поле, давление, температуpa).
Симметрия кристаллов
Свойство кристаллов совмещаться с собой при поворотах, отражениях, параллельных переносах либо при части или комбинации этих операций. Симметрия внешней формы (огранки) кристалла определяется симметрией его атомного строения, которая обусловливает также и симметрию физических свойств кристалла.

На рисунке изображён кристалл кварца. Внешняя его форма такова, что поворотом на 120° вокруг оси 3 он может быть совмещён сам с собой.
Скалярное поле Скалярная функция  φ (M)  положения точки, заданная в некоторой области пространства.
Примеры
  • Плотность распределения заряда.
  • Плотность распределения массы.
  • Температура неоднородно нагретого тела.
  • Потенциал системы заряженных частиц.
  • Потенциальная энергия тела, обусловленная гравитацией.
    		•
    Скалярное произведение векторов Число, равное произведению длин векторов на косинус угла между ними:
    a · b = | a | · | b | cos φ.

    Скалярное произведение векторов  a  и  b  можно представить в виде суммы попарных произведений соответствующих координат этих векторов:
    a · b = ax bx + ay by + az bz
    Пример Пусть  a = {3,–1, 2}  и  b = {5,4,3}. Тогда  a · b = 17.
    Смешанное произведение векторов Произведению вида  a · (b × c).

    Смешанное произведение векторов  a ,  b  и  c  можно представить в виде определителя третьего порядка, составленного из координат этих векторов: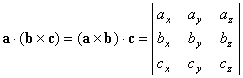

    Интерпретация Смешанное произведение векторов  a ,  b  и  c  с точностью до знака равно объему параллелепипеда, построенного на этих векторах.
    Собственные колебания
    		Колебания колебательной системы, совершаемые при отсутствии внешнего воздействия за счёт первоначально сообщённой энергии (потенциальной или кинетической, например, в механических системах через начальные смещения или начальные скорости).

    Характер собственных колебаний определяется главным образом собственными параметрами системы (массой, индуктивностью, ёмкостью, упругостью и др.).
    В реальных системах собственные колебания всегда затухающие вследствие рассеяния энергии, а при больших её потерях - апериодические. В линейных системах собственные колебания представляют собой суперпозицию нормальных колебаний.
    Спектроскопия
    		Область физики, посвящённая исследованию распределения интенсивности электро-магнитного излучения по длинам волн или частотам.

    Характер собственных колебаний определяется главным образом собственными параметрами системы (массой, индуктивностью, ёмкостью, упругостью и др.).
    По диапазонам длин волн (в порядке убывания) или частот (в порядке возрастания) выделяют: радиоспектроскопию, микроволновую спектроскопию, субмиллиметровую спектроскопию, инфракрасную спектроскопию, оптическую спектроскопию (включающую ближнюю ИК-, видимую и частично УФ-области спектра и выделенную главным образом по прозрачности оптических материалов - стекла, кварца и др.), ультрафиолетовую спектроскопию, рентгеновскую спектроскопию.
    Стокса формула Циркуляция векторного поля  A  вдоль замкнутого контура  L  равна потоку ротора  A  через поверхность  S, натянутую на контур  L :

    Примеры Формула Грина
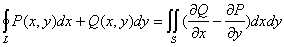
    представляет собой частный случай формулы Стокса.
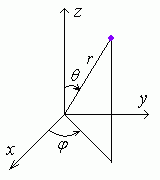
    Сферические координаты Тройка чисел  0 ≤ r < ∞ ,  0 ≤ φ < 2π ,  0 ≤ θ ≤ π , связанных с декартовыми координатами соотношениями

    x = r sin θ cos φ ,    y = r sin θ sin φ ,     z = r cos θ .

    Элемент объема в сферических координатах равен

    d V = r2 sin θ dθ dr dφ

    Иллюстрация
    Сферическое поле
    		См. Центральное скалярное поле.