П   
Пар
Газообразное состояние, в которое переходит вещество в результате испарения, сублимации или кипения.

Обычно пар находится в контакте с конденсированной фазой. Понятия газа и пара почти полностью эквивалентны; к газам относят вещества при температуре выше критической, поэтому при повышении давления газ не переходит в конденсированное состояние.
Процесс конденсации возможен лишь из парообразного состояния, т. е. при температуре ниже критической.
Парциальное давление
Часть общего давления, относящаяся к одному из компонентов газовой смеси. Равно давлению, которое он оказывал бы в отсутствие всех других компонентов смеси, т. е. в том случае, когда масса данного компонента, содержащаяся в газовой смеси, одна занимала бы весь объём.
Понятие парциального давления применимо только к идеальным газам.
Паскаля закон
Основной закон гидростатики, согласно которому давление на поверхности жидкости, произведённое внешними силами, передаётся жидкостью одинаково во всех направлениях. Установлен Б. Паскалем, опубликован в 1663.
Плавание тел
Состояние равновесия твёрдого тела, частично или полностью погружённого в жидкость (или газ).
Основная задача теории плавания тел - определение равновесия тела, погружённого в жидкость, выяснение условий устойчивости равновесия. Простейшие условия плавания тел указывает закон Архимеда.

Если тело погрузить в жидкость до какой-нибудь плоскости возможной грузовой ватерлинии ab (см. рис), то на тело будут действовать направленная перпендикулярно этой плоскости (т. е. вертикально вверх) выталкивающая сила F, проходящая через центр А, и численно равная ей сила тяжести Р.
Как доказывается в теории плавания тел, направление силы F совпадает одновременно с направлением нормали n к поверхности II в точке А.

Плазма
Частично или полностью ионизованный газ, в котором плотности положительных и отрицательных зарядов практически одинаковы.
Поверхности уровня Множество всех точек пространства с одинаковыми значениями скалярного поля.
Пример

Рис. 1. Сечение поверхностей уровня плоскостью, проходящей через точки расположения зарядов.
Поверхностный интеграл первого рода Интеграл от скалярной функции  f  по поверхности  S :  
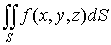
Интерпретация Если функция  f  описывает плотность распределения заряда вдоль поверхности  S, то интегрирование этой функции по области  S  дает величину заряда поверхности.
Поверхностный интеграл второго рода Интеграл по поверхности  S  от проекции векторной функции  A  на направление нормали к  S :

Пример Если векторную функцию  A(x, y, z)  интерпретировать как скорость течения жидкости, то интегрирование этой функции по области  S  дает объем жидкости, протекающей в единицу времени через поверхность  S.
Поле векторное
Векторная функция  A (M)  положения точки  M, заданная в некоторой области пространства.

В прямоугольной системе координат положение точки определяется декартовыми координатами  x,  y  и  z. Поэтому задание векторного поля  A (M)  равносильно заданию векторной функции  A (x, y, z).
Примеры
  • Сила, действующая на единичный положительный заряд со стороны других зарядов (напряженность электрического поля).
  • Сила, действующая на движущийся заряд со стороны других движущихся зарядов. (Индукция магнитного поля.)
  • Сила гравитационного притяжения.
  • Скорость частиц движущейся жидкости.
    		•
    Поле потенциальное Векторное поле  A, которое может быть представлено в виде градиента некоторого скалярного поля φ:
    A = grad φ.
    Примеры
  • Сила гравитационного притяжения тела
  • Напряженность электрического поля
    		•
    Поле скалярное Скалярная функция  φ (M)  положения точки, заданная в некоторой области пространства.
    Примеры
  • Плотность распределения заряда.
  • Плотность распределения массы.
  • Температура неоднородно нагретого тела.
  • Потенциал системы заряженных частиц
  • Потенциальная энергия тела, обусловленная гравитацией.
    		•
    Поток векторного поля через поверхность Поверхностный интеграл второго рода от векторной функции A(x, y, z) по поверхности S:

    (n – нормаль к поверхности).
    Пример Поток векторного поля  E = r/r3  через поверхность сферы радиуса  R равен 4π.
    Производная скалярного поля по направлению вектора Скорость изменения скалярного поля φ в направлении, заданном вектором:
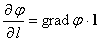
    Пример Пусть  φ = 1/r, где  r  – величина радиус-вектора  r.
    Тогда производная скалярного поля φ по направлению вектора  r равна  1/r2.