|
|
| Уравнения Лагранжа |
|
|
|
|
|
Обратимяся к проблеме описания движения частиц в классической механике.
Рассмотрим функционал вида
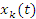 и скорости и скорости
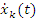 частиц, а функцию F – как Лагранжиан
L системы (разность между кинетической и потенциальной энергией системы частиц). частиц, а функцию F – как Лагранжиан
L системы (разность между кинетической и потенциальной энергией системы частиц).
В результате функционал J принимает вид
Согласно принципу Гамильтона (другое название которого – принцип наименьшего действия), движение системы с момента времени t1 до момента t2 происходит таким образом, что действие S принимает наименьшее значение (экстремальное значение). Ранее было показано (см. Обобщение уравнения Эйлера), что задача о нахождении экстремали, на которой функционал (1) достигает своего наибольшего или наименьшего значения (в классе функций с фиксированными границами), может быть сформулирована в виде системы уравнений Эйлера:
В декартовых координатах частные производные Кроме того, принцип Гамильтона находит плодотворное применение и в других областях физики, например, в квантовой механике и электродинамике. Наконец, координаты 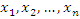 понимаются в широком смысле – как обобщенные координаты
q1, q2, ..., qn, в частности, как
цилиндрические или сферические координаты частиц. В терминах обобщенных координат
q1, q2, ..., qn
и обобщенных скоростей понимаются в широком смысле – как обобщенные координаты
q1, q2, ..., qn, в частности, как
цилиндрические или сферические координаты частиц. В терминах обобщенных координат
q1, q2, ..., qn
и обобщенных скоростей
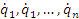 уравнения Лагранжа имеют вид
уравнения Лагранжа имеют вид
|
|
|