Обратимся вновь к основным положения алгебры векторов трехмерного пространства, абстрагируясь от природы элементов, над которыми выполняются операции их сложения и умножения на число.
Другими словами, давайте на какое-то время отвлечемся от истинного понятия векторов, подразумевая далее под ними некие абстрактные объекты.
Кроме того, свойства линейных операций над векторами, которые фактически вытекают из соответствующих определений, будем в дальнейшем интерпретировать как изначально заданный свод правил.
Пусть V – некоторое непустое множество. Назовем элементы этого множества (абстрактными) векторами и сохраним за ними стандартные обозначения векторов в виде a, b, c, ...
Предположим, что для векторов множества V определены линейные операции, а именно:
-
Задано правило, которое любым двум векторам a и b множества V ставит в соответствие некоторый вектор c этого же множества, называемый их суммой:
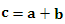 . .
-
Задано правило умножения произвольного вектора a на вещественное (или комплексное) число
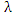 . .
Учитывая, что сложение векторов обычного трехмерного пространства обладает свойствами коммутативности и ассоциативности, потребуем сохранения этих свойств и применительно к операции сложения абстрактных векторов множества V:
| |
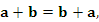
|
(1) |
|
| |
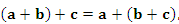
|
(2) |
|
Множество V называется векторным пространством (или линейным пространством), если эти линейные операции удовлетворяют двум аксиомам.
Аксиома 1 устанавливает свойства коммутативности и ассоциативности относительно операции сложения векторов (равенства (2) и (3)), существование нулевого вектора (равенство (4)), а также существование противоположного вектора (– a) для каждого вектора a из множества V (равенство (5)):
Аксиома 2 формулирует условия, которым должны удовлетворять операции умножения векторов на числа:
Отметим, что различают вещественное и комплексное векторные пространства – в зависимости от того, на какие числа допускается умножение элементов пространства.
Приведем примеры векторных пространств.
-
Множество всех векторов на прямой со стандартными операциями сложения векторов и их умножения на вещественные числа образует вещественное векторное пространство
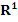 . .
-
Множество всех векторов плоскости образует векторное пространство
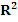 . .
-
Множество всех векторов трехмерного пространства образует векторное пространство
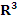 . .
-
Множество всех строчных матриц размера 1×n образует векторное пространство.
-
Множество всех столбцовых матриц размера n×1 образует векторное пространство.
Таким образом, понятие векторного пространства определяется не природой образующих его элементов, а правилами действий над этими элементами, в качестве которых могут выступать реальные векторы, матрицы, функции или иные математические объекты.
|