Математический аппарат векторной алгебры может с успехом применяться для описания самых разнообразных математических объектов и обладает большим потенциалом своего обобщения, например, на случай векторных пространств произвольной размерности. Дело в том, что многие математические величины имеют одинаковые свойства и правила действий над ними. В частности, правило матричного умножения “строка на столбец” по своей сути идентично скалярному произведению векторов, выраженному в некоторой ортогональной системе координат.
Важной составляющей математического аппарата векторной алгебры является разложение вектора по базисному набору, что позволяет сводить действия над векторами к соответствующим операциям над векторами базисного набора, а в конечном итоге - над координатами векторов. Подобный подход оказывается весьма продуктивным и широко применяется для решения задач линейной алгебры, теории дифференциальных уравнений и математического анализа.
Выделим ключевые положения алгебры векторов трехмерного пространства.
-
Для векторов
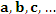 определена операция их сложения, которая каждой паре векторов a и b ставит в соответствие вектор c = a + b, называемой суммой векторов a и b. определена операция их сложения, которая каждой паре векторов a и b ставит в соответствие вектор c = a + b, называемой суммой векторов a и b.
Для любого вектора определена операция умножения на вещественное число 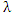 , которая вектору a ставит в соответствие вектор c = λa. , которая вектору a ставит в соответствие вектор c = λa.
-
Свойства операции сложения векторов:
| |
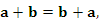
|
(коммутативность)
|
(1) |
|
| |
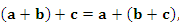
|
(ассоциативность)
|
(2) |
|
| |
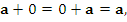
|
(существование нулевого вектора)
|
(3) |
|
| |
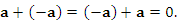
|
(существование противоположного вектора)
|
(4) |
|
-
Свойства операции умножения вектора на число:
| |
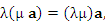
|
(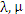 - вещественные числа) - вещественные числа)
|
(5) |
|
| |
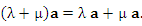
|
(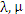 - вещественные числа) - вещественные числа)
|
(6) |
|
| |
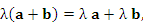
|
(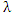 - вещественное число) - вещественное число)
|
(7) |
|
-
Для векторов a и b определена операции их скалярного произведения:
| |
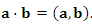
|
(8) |
|
Скалярный квадрат 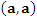 задает норму задает норму 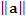 вектора a, определяемую выражением вектора a, определяемую выражением
| |
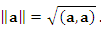
|
(9) |
|
-
Пусть векторы
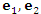 и и 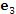 образуют ортонормированный базис трехмерного векторного пространства: образуют ортонормированный базис трехмерного векторного пространства:
| |
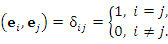
|
(10) |
|
Тогда любой вектор a этого пространства может быть представлен в виде разложения
| |
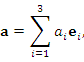
|
(11) |
|
где 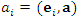 – координаты вектора a в базисе – координаты вектора a в базисе 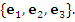 . .
Для удобства последующего изложения назовем набор правил, сформулированных в виде равенств (1)-(4), аксиомой 1, а совокупность правил вида (5)-(7) будем называть аксиомой 2.
|