|
Говорят, что ранг матрицы A размера m×n равен r, если существует хотя бы одна несингулярная подматрица r-го порядка, тогда как любая подматрица более высокого порядка является сингулярной.
Если это определение озвучить в терминах определителей, то оно будет выглядеть примерно так:
Матрица A размера m×n имеет ранг r, если существует хотя бы один отличный от нуля определитель r-го порядка, тогда как определитель любой подматрицы более высокого порядка равен нулю. Очевидно, что
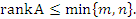
Для вычисления ранга матрицы можно использовать метод элементарных преобразований строк и столбцов – в точности тот самый метод, который применяется для вычисления определителей. Будет уместным напомнить основные операции метода:
-
Перестановка строк или столбцов.
-
Умножение строки или столбца на ненулевое число.
-
Прибавление к строке (столбцу) другой строки (столбца), предварительно умноженной на любое число.
-
Нулевая строка или столбец вычеркивается.
Целью элементарных преобразований является приведение матрицы к ступенчатой форме, т.е. к квазитреугольному виду - типа того, что представлено ниже:
| |
 . .
|
(1) |
|
Очевидно, что определитель третьего порядка, составленный из элементов первых трех строк и столбцов, отличен от нуля, и ранг матрицы равен 3:

Отметим, что любая матрица может быть представлена посредством эквивалентных преобразований (в смысле неизменности ее ранга) к блочному виду
| |

|
(2) |
|
где E - единичная матрица.
Например, для преобразования матрицы (1) к такому виду достаточно прибавить ко второму, третьему и пятому столбцам первый столбец с соответствующим образом подобранными коээффициентами, что приведет нас к матрице
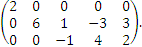
Фактически, результаты этих преобразований чрезвычайно просты: во всех позициях первой строки - кроме первой - элементы превратились в нулевые.
Прибавляя затем второй столбец к третьему, четвертому и пятому - с соответствующим образом подобранными коээффициентами, получим
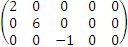
Далее поделим каждую строку на соответствующий коэффициент и удалим нулевые столбцы:
| |
 . .
|
(3) |
|
Рассматриваемая матрица приведена к вышеуказанному виду.
|