Теорема об обратной матрице

Теорема об обратной матрице

      Показано, что обратная матрица существует только для несингулярной матрицы.

      При этом для одной и той же матрицы не могут существовать две различные обратные матрицы.

      Сформулирован алгоритм вычисления обратной матрицы.

Теорема. Для любой несингулярной матрицы A существует единственная обратная матрица: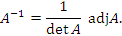

Сингулярная матрица не имеет обратной матрицы.

Доказательство.

Предположим, что для матрицы A существует обратная матрица . Тогда
.
Учитывая, что определитель произведения матриц равен произведению определителей, получаем

и, следовательно,
Это означает, что сингулярные матрицы не имеют обратных матриц.
Предположим теперь, что существуют две обратные матрицы, и . Тогда

и

Используем эти равенства для преобразования матрицы :

что доказывает утверждение об единственности обратной матрицы.

В соответствии с Леммой 2

Следовательно,