Лемма 2   
      Пусть  A – квадратная матрица  n-го порядка.

      Утверждение. Если , то

  (3)  
где  E  – единичная матрица.

      Доказательство. Запишем равенства (3) в терминах матричных элементов:

  (4)  

      Это означает, что

  (5)  

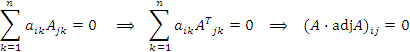
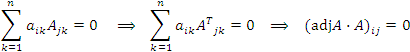
      Предположим, что . Тогда согласно Лемме 1

и

      Мы показали, что результатом умножения (в том или ином порядке) матрицы  A  и присоединенной матрицы  является диагональная матрица. Остается доказать, что все диагональные элементы этой матрицы равны :

      Этот результат становится очевидным, если воспользоваться теоремами о разложении определителя по элементам строки и столбца: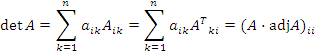

и