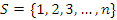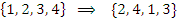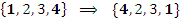Перестановки и транспозиции

Перестановки и транспозиции

Расположение первых n натуральных чисел в порядке их возрастания определяется в качестве эталонного, а любой другой порядок размещения этих чисел - как перестановка "нормального" расположения.

Оказывается, что произвольная перестановка таких чисел может быть получена из нормальной перестановки посредством некоторого числа транспозиций, то есть переменами позиций одной пары элементов перестановки при сохранении позиций остальных элементов.

Рассмотрим множество S натуральных чисел от 1 до n, расположенных в порядке возрастания (в естественном порядке):

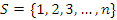
Под перестановкой множества S понимается множество этих же чисел, упорядоченное некоторым другим образом:

Перестановка называется транспозицией, если переставляются местами только два элемента множества, тогда как остальные элементы остаются на своих местах.

Пример перестановки: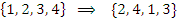

Пример транспозиции: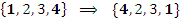

Любую перестановку множества S можно осуществить посредством нескольких транспозиций. Например, перестановка {2,4,1,3} является результатом трех транспозиций множества S :

Говорят, что перестановка множества S содержит инверсию элементов i_j и i_k , если нарушен их естественный порядок расположения, т.е. больший элемент расположен левее меньшего:

i_j > i_k ( j < k ).

Например, перестановка {2, 4, 1, 3} содержит три инверсии элементов:

2    и    1,
4    и    1,
4    и    3.

Число инверсий определяет четность перестановки. Перестановка называется четной, если она содержит четное число инверсий элементов. Нечетная перестановка содержит нечетное число инверсий.

Заметим, что четная перестановка может быть преобразована к естественному порядку посредством только четного числа транспозиций, тогда как для преобразования нечетной перестановки к естественному порядку требуется нечетное число транспозиций. (Это утверждение является следствием Теоремы 1, см раздел "Теоремы о транспозициях и перестановках".)

Пример: Перестановка {2, 4, 1, 3} является нечетной, поскольку содержит 3 инверсии элементов.
Можно также сказать, что перестановка {2, 4, 1, 3} является нечетной, поскольку представляет собой последовательность трех транспозиций.