Proof: If is a bounded sequence, then there exists a finite positive number M such that

for all natural n.

Let be an infinitesimal sequence. Then for any arbitrary small , the positive number corresponds to a suitable natural number N such that

for each n>N.

Therefore,

,

whenever n>N. Hence, the desired proposition.

Property 2

explanation

Proof: Let and be infinitesimal sequences.

Then for any positive , the number corresponds to natural numbers and such that

for each and

for each .

If number N is not less than each of numbers and then

for any arbitrary small whenever n>N.

Property 2 Corollary

explanation

Proof: Let us apply the Mathematical Induction Principle.

Let be the sequence of statements for n = 2, 3, 4, ... such that the sum of n infinitesimals is an infinitesimal.

Induction basis: By Property 2, the statement is true for n=2.

Induction hypothesis: Assume that the statement holds true for some integer .

Induction step: Consider the sum of (n+1) infinitesimals. By the hypothesis, the sum of n infinitesimals is an infinitesimal, and so the given sum can be considered as consisting of two infinitesimal items. But the sum of two infinitesimals is also an infinitesimal.

Therefore, the statement implies the statement , and hence is true for any integer .

Property 3

explanation

Proof: Let be an infinitesimal sequence.

Then for any there exists a number N such that

,

which implies

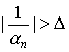
for each n>N.

Hence, is an infinite large sequence.

Likewise, if is an infinite large sequence then any corresponds to a number N such that

,

and so

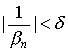
whenever n>N.

Hence, is an infinitesimal sequence.