Let 
be any vectors and let 
be numbers. Then the expression of
the form
is called a linear combination of the vectors 
.
If there exists a non-trivial solution of the equation
 |
with respect to 
, then the set of vectors 
is linear dependent. Otherwise, if
equation (*) has only the trivial solution
then 
is the set of linear independent
vectors.
In other words, the set of vectors is linear dependent if one of the
vectors can be expressed as a linear combination of the others. Indeed,
assume that 
. Then from equation (*)
it follows that
,
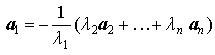just as expected.
| Theorem |
|
1) Any two non-zero vectors are linear dependent if and only if they are collinear. 2) Any three non-zero vectors are linear dependent if and only if they are coplanar. 3) Any four vectors are linear dependent. |
Corollary: Let a1, a2 and a3 be three non-coplanar vectors. Then any vector b can be expressed as a linear combination of a1, a2 and a3:
.
