| Property 1 |
The rows and columns of determinants have equal rights, that is,
.
| Property 2 |
 |
Multiplying any row or column of a determinant by a number 
, multiplies the determinant by that
number:
This means that the common factor of a row (or column) can be taken outside the sign of a determinant.
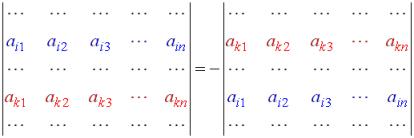
| Property 3 |
|
Interchanging any two rows (or columns) of a matrix changes the sign of the determinant:
| Property 4 |
|
If a determinant has a zero-row or zero-column then the determinant is equal to zero:
| Property 5 |
|
If a determinant has two rows (or columns) equal then the determinant is equal to zero:
| Property 6 |
|
If two rows (or columns) of a determinant are proportional to each other then the determinant is equal to zero:
| Property 7 |
|
If each element of a row (or column) of a determinant is the sum of two items then
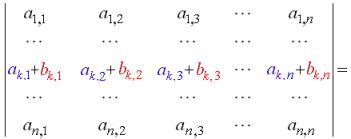
| Property 8 |
|
A determinant holds its value if a row (column) multiplied by a number is added to another one:
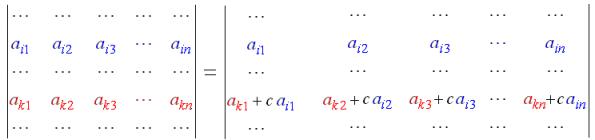
| Property 9 |
|
Let A and B be square matrices of the same order. Then the determinant of the product is equal to the product of the determinants:
.
| Property 10 |
|
The determinant of a triangular matrix is equal to the product of the diagonal elements:
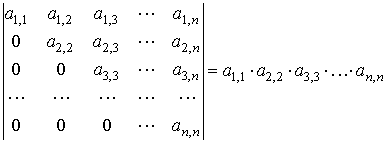
In particular, the determinant of an identity matrix is equal to unity.
