Let .
Verify that .

Solution:

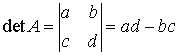and

That is O.K.

Example 2

Let 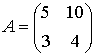. Apply the properties of determinants to evaluate det A.

Solution:

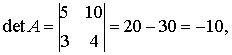
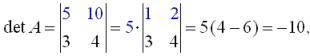
Example 3

Compare determinants and .

Solution:

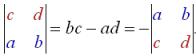
Example 4

Evaluate the below determinant

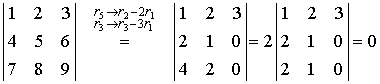
Example 5

Let 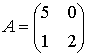and .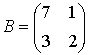

Verify that

Solution:

.

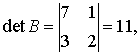
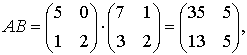
That is O.K.

Example 6

Evaluate , if

.

Solution:

First,

.

Then,

.

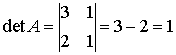Finally,

.

Example 7

Let .

Calculate a) , b) , c) , d) , e) .

Solution:

a) The determinant of a matrix in the triangular form equals the product of the diagonal elements. Therefore,

.

b) The determinant of the product of matrices is equal to the product of the determinants, and so

.

c) Let I be the identity matrix of the third order. Then

.

d) Likewise the above,

.

e) Simplify the matrix :

.

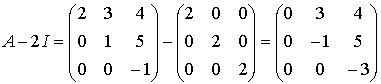Therefore, .