Property 1

Let x be the abscissa of a point of hyperbola (8). Then the focal distances of the point are the following:

,

(9a)

.

(9b)

Proof: To prove this property we use a similar way as in case of ellipse.

The distance between two points and is

,

where

,

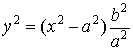and .

Therefore,

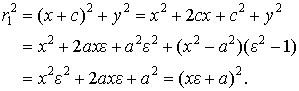
Likewise,

.

Since for points on the right half-hyperbola, and for points on the left half-hyperbola, we have the desired results.

Property 2

For any point of hyperbola (8), the difference between the focal distances is the constant quantity:

.

(10)

The sign depends on whether the point lies on the right or left half-hyperbola.

The proof is straightforward. We only need to apply Property 1.

The directrices of hyperbola (8) are two vertical lines .

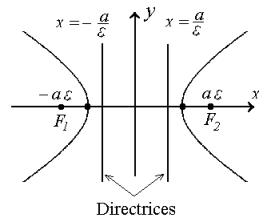
Property 3

The ratio of the distances from a point of hyperbola (8) to a focus and to the corresponding directrix is equal to the eccentricity of the hyperbola.

.

(11)

Property 4

Two straight lines are the asymptotes of hyperbola (8).

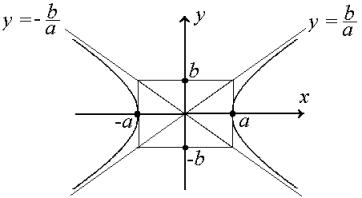
Proof: Express the variable y from equality (8) in the explicit form.

.

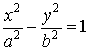
If x approaches infinity, then constant is a negligible quantity, that is,

.

Hence, the property.

Property 5

Assume that the curve of a hyperbola has the mirror reflection property. If a point light source is located at a focus of the hyperbola, then the other focus is the image source of rays that being reflected.

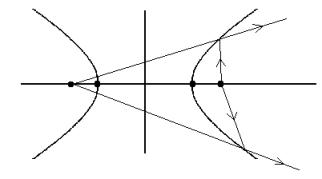
The above drawing illustrates that reflected rays form a divergent beam.
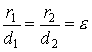