A hyperbola is a plane curve, which can be represented by one of the equations

(7)

in some Cartesian coordinate system.

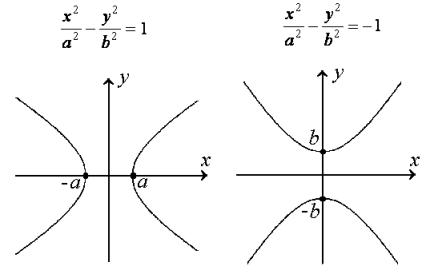
Equations (7) are called the canonical equations of the hyperbola.

In this system, the coordinate axes are axes of symmetry, and so if a point (x,y) belongs to the hyperbola then the points (-x,y), (x,-y) and (-x,-y) also belong to the hyperbola.

The intersection points of the hyperbola with the axis of symmetry are called the vertices of the hyperbola. Any hyperbola has two vertices.

If a = b then the hyperbola is called an equilateral hyperbola.

The equations

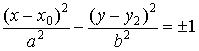
describe hyperbolas with the center is at the point . The axes of symmetry of these hyperbolas pass through , being parallel to the coordinate axes.

Consider a hyperbola, which is given by the equation

.

(8)

Two fixed points, and , are called the focuses of the hyperbola, where .

Correspondingly, the distances r1 and r2 from any point M(x,y) of the hyperbola to the points F1 and F2 are called the focal distances.

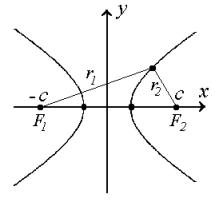
The ratio is called the eccentricity of hyperbola.

Note that .
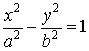