Словарь физических терминов

Б

Базис в трехмерном пространстве	Любая тройка некомпланарных векторов e₁, e₂, e₃. Произвольный вектор b трехмерного пространства может быть представлен, и притом единственным образом, в виде линейной комбинации базисных векторов: b = b₁e₁ + b₂e₂ + b₃e₃.
Пример	Единичные попарно ортогональные векторы i, j и k образует базис в трехмерном пространстве. Тройку таких векторов обычно выбирают так, чтобы их направления совпадали с направлениями координатных осей прямоугольной системы координат, а разлзложение произвольного вектора по базисному набору векторов i, j и k записывают в виде b = b_x i + b_y j + b_z k. Коэффициенты b_x , b_y и b_z называются координатами вектора b в ортогональном базисе векторов.

Базис кристаллической структуры	Полная совокупность координат центров атомов в симметрично независимой области кристаллической структуры. Центры атомов в любой идеальной кристаллической структуре образуют одну (в простейших случаях) или несколько правильных систем точек, которые в каждой федоровской группе подразделяются на позиции Уайкова. Две правильные системы точек относятся к одной позиции Уайкова, если они имеют точки, принадлежащие одному и тому же элементу симметрии (частные правильные системы точек), либо находятся в общем положении (общие правильные системы, к которым причисляются точки, принадлежащие скользящим плоскостям симметрии и винтовым осям). Различные позиции Уайкова для каждой из 230 фёдоровских групп приведены в Международных таблицах по кристаллографии. Каждая правильная система содержит одну точку в независимой области.

Бар	Внесистемная единица давления, применявшаяся главным образом в метеорологии: 1 бар = 10⁵ Па = 0,986923 атм. Баром также называлась единица давления в СГС системе единиц (1 бар = 1 дин/см²).

Безызлучательный квантовый переход	Квантовый переход, который в противоположность излучательному квантовому переходу не связан с процессами излучения, то есть с испусканием или поглощением фотонов (а также с комбинационным рассеянием света). При безызлучательном квантовом переходе изменение энергии системы (её отдача при переходе из состояния с большей энергией в состояние с меньшей энергией и получение при обратном переходе) осуществляется благодаря непосредственному взаимодействию данной системы с другими системами. Например, частица в газе может отдавать энергию или получать её (возбуждаться) при столкновениях с другими частицами. В жидкости или твёрдом теле частица (молекула, ион) взаимодействует с ближайшим окружением и её электронная энергия возбуждения может при безызлучательном квантовом переходе перейти в колебательную и другие виды энергии (то есть расходуется на возникновение элементарных возбуждений - фононов и др. квазичастиц). Возможны также безызлучательные квантовые переходы без изменения энергии системы, связанные с её спонтанным распадом, например, автоионизация атома при оже-эффекте или предиссоциация молекул.

Биения	Периодические изменения во времени амплитуды колебания, возникающего при сложении двух гармонических колебаний с близкими частотами. Биения появляются вследствие того, что величина разности фаз между двумя колебаниями с различными частотами всё время изменяется так, что оба колебания оказываются в какой-то момент времени в фазе, через некоторое время в противофазе, затем снова в фазе и так далее. Соответственно амплитуда результирующего колебания периодически достигает то максимума, равного сумме амплитуд складываемых колебаний, то минимума, равного разности этих амплитуд. Например, биения возникают при звучании двух камертонов с близкими частотами - звук поочерёдно усиливается и ослабевает, при сложении нормальных колебаний с близкими частотами в связанных линейных осцилляторах. Измерение тона биения лежит в основе точных измерений малых разностей двух близких частот, в частности сравнения некоторой измеряемой частоты с эталонной.

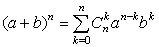
Бином Ньютона	Формула возведения в целую степень суммы двух чисел: 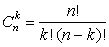Биномиальные коэффициенты обладают следующими свойствами: , , .
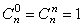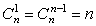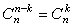Пример	(a + b)³ = a³ + 3a² b + 3a b² + b³

Бозе-газ	Газ из частиц, подчиняющихся квантовой Возе - Эйнштейна статистике. Бозе-газом являются, например, ⁴He, атомы которого содержат чётное число нуклонов, и газы фотонов (квантов электро-магнитного поля) и некоторых квазичастиц, например фононов (элементарных возбуждений кристаллич. решётки). Если можно пренебречь взаимодействием между частицами, Бозе-газ называется идеальным. В идеальном Бозе-газе при температуpax ниже вырождения температуры наступает Бозе - Эйнштейна конденсация, при которой макроскопически большое число частиц обладает нулевым импульсом (образует бозе-конденсат).

Бора постулаты	Основные положения о существовании стационарных состояний и о квантовых переходах с излучением, введённые H. Бором (N. Bohr) в 1913 в его квантовой теории атома.

Браве решётки	Классификация решёток параллельных переносов, учитывающая как их точечную, так и параллельно-переносную симметрию. Две решётки относятся к одному и тому же типу Браве, если их параллелепипеды Браве одинаковы и имеют одинаковую центрировку. Всего существует 14 типов Браве решёток, названных по имени О. Браве (A. Bravais), строго обосновавшего эту классификацию.

Браве репер	Система координат, построенная на векторах решётки, совпадающих с наиболее симметричными в данной голоэдрии направлениями.

Бриллюэна зона	Ячейка обратной решетки кристалла, содержащая все трансляционно-неэквивалентные точки. Поскольку состояния квазичастиц твёрдого тела, в которых значения квазиимпульсов отличаются на один из векторов трансляции обратной решётки, являются эквивалентными, то Бриллюэна зона выделяет в пространстве квазиимпульсов области, включающие в себя все неэквивалентные значения квазиимпульсов, характеризующих состояние квазичастиц.