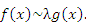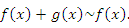Пусть  и и  – бесконечно большие функции при x → a. Рассмотрим возможные значения предела отношения этих функций: – бесконечно большие функции при x → a. Рассмотрим возможные значения предела отношения этих функций:
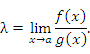
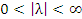 , то функции , то функции  и и  называются бесконечно большими одного и того же порядка. называются бесконечно большими одного и того же порядка.
Функции  и и  называются эквивалентными бесконечно большими при x → a, если λ = 1. Для записи эквивалентности функций используется обозначение вида называются эквивалентными бесконечно большими при x → a, если λ = 1. Для записи эквивалентности функций используется обозначение вида
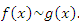
 называется бесконечно большой более высокого порядка по сравнению с называется бесконечно большой более высокого порядка по сравнению с  при x → a, если λ = ∞; при этом говорят, что при x → a, если λ = ∞; при этом говорят, что  имеет меньший порядок роста. имеет меньший порядок роста.
Если  и и 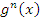 представляют собой бесконечно большие функции одного и того же порядка, то функция представляют собой бесконечно большие функции одного и того же порядка, то функция  называется бесконечно большой n-го порядка по сравнению с называется бесконечно большой n-го порядка по сравнению с  . Например, функция . Например, функция 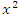 является бесконечно большой 4-го порядка по сравнению с является бесконечно большой 4-го порядка по сравнению с 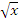 при x → ∞. при x → ∞.
Если λ = 0, то бесконечно большие функции  и и  меняются своими ролями. В этом случае функция меняются своими ролями. В этом случае функция  является бесконечно большой более высокого порядка по сравнению с является бесконечно большой более высокого порядка по сравнению с  при x → a. при x → a.
Свойства эквивалентных бесконечно больших функций.
|
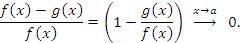
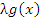 являются эквивалентными бесконечно большими функциями:
являются эквивалентными бесконечно большими функциями: