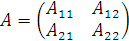Произведение матриц

Произведение матриц

    Предположим, что нам нужно умножить матрицу A на матрицу B.

    Чтобы свести эту проблему к уже известной ("Умножение строки на столбец"), матрицу A будем рассматривать как набор строк, тогда как матрицу B - как набор столбцов.

    Тогда все, что нам предстоит проделать - это умножить каждую строку матрицы A на каждый столбец матрицы B. При этом номера перемножаемых строк и столбцов сохраняют свою силу - в том смысле, что результат умножения, например, пятой строки на третий столбец записывается в пятую строку на третий столбец.

Пример:

Пусть

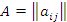– m×l матрица и пусть

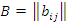– l×n матрица.

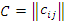Тогда произведением AB называется матрица

размера m×n , элементы

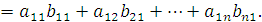
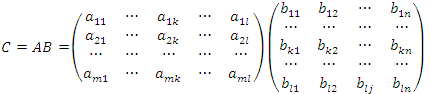
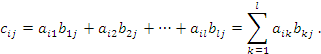
которой вычисляются по правилу умножения i-ой строки матрицы A на j-ый столбец матрицы B:

(1а)

(1б)

Если обозначить строки матрицы A символами

, а столбцы матрицы B – символами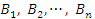

, то правило (1) матричного умножения можно представить в следующем блочном виде:

(2)

Таким образом, если матрица A содержит m строк, а матрица B содержит n-столбцов, то произведение AB представляет собой матрицу С размера m × n. Элемент

, стоящий в i-ой строке и j-ом столбце матрицы AB, вычисляется по правилу умножения строки на столбец: i-ая строка матрицы A умножается на j-ый столбец матрицы B.

Операция матричного умножения определена только для матриц, удовлетворяющих определенным условиям:

Произведение AB определено, если число столбцов матрицы A совпадает с числом строк матрицы B. (Другими словами, число элементов в строке матрицы A должно совпадать с числом элементов в столбце матрицы B.)
Произведение BA определено, если число столбцов матрицы B совпадает с числом строк матрицы A.

Отметим, что в общем случае произведение матриц некоммутативно, то есть AB ≠ BA. Более того,

Существование одного из произведений (AB или BA) не влечет за собой существование другого.
Если определено каждое из таких произведений, то размеры матриц AB и BA не обязательно совпадают друг с другом. Например, результатом умножения матрицы A размера 1×n на матрицу B размера n×1 является число (то есть матрица размера 1×1), тогда как произведение BA представляет собой квадратную матрицу n-го порядка.
Если матрицы A и B являются квадратными маирицами n-го, то и их произведения AB и BA являются матрицами такого же порядка. Однако даже для таких матриц их произведения в одном и другом порядках равны только в некоторых частных случаях.
Произведение нескольких матриц, расположенных в определенном порядке, однозначно определено, если число столбцов каждой матрицы равно числу строк соседней матрицы справа. В этом случае для нахождения произведения матриц можно использоать произвольный порядок расстановки скобок (см Свойства матричных операций).

Разность AB – BA произведений квадратных матриц одного и того же порядка называется коммутатором матриц.
Сумма AB + BA произведений квадратных матриц одного и того же порядка называется антикоммутатором матриц.

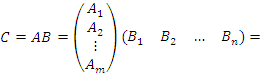
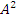Символическая запись означает произведение двух одинаковых квадратных матриц:
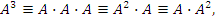
Аналогичным образом определяются другие целые положительные степени квадратной матрицы:

. (3)

Правило (1) матричного умножения сохраняет свой вид и в том случае, когда элементами матриц A и B являются другие матрицы. Пусть, например, матрицы A и B представлены в виде

(4)

где A_i j и B_i j – некоторые матрицы, размеры которых таковы, что соответствующие матричные произведения определены.
Тогда

(5)