|
|
| Математический маятник |
|
|
|
|
|
Рассмотрим малые колебания математического маятника.
Для анимации изображения используйте клавиши панели управления рисунка. Выберем в качестве обобщенной координаты угол φ, образуемый нитью с вертикальной прямой и составим Лагранжиан:
Уравнение Лагранжа имеет вид:
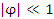 ), то ), то 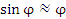 , что влечет , что влечет
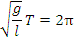 . .
Тогда
|
|
|