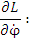|
Пример 1. Рассмотрим движение частицы в плоском центральном поле. Составим Лагранжиан в полярных координатах
r и φ. Учитывая соотношения
| |
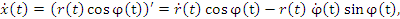
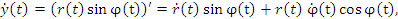
|
(1) |
|
находим кинетическую энергию частицы:
| |
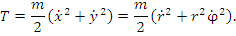
|
(2) |
|
Потенциальная энергия V частицы в центральном поле зависит только от расстояния r от центра
и, таким образом,
| |
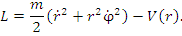
|
(3) |
|
Первое уравнение Лагранжа
| |
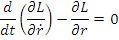 . .
|
(4) |
|
приводится к виду
| |
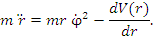
|
(5) |
|
Поскольку переменная φ не входит явным образом в выражение для Лагранжиана, то
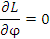 и, следовательно, второе уравнение Лагранжа и, следовательно, второе уравнение Лагранжа
| |
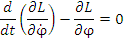
|
(6) |
|
выражает сохранение обобщенного импульса 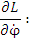
| |
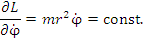
|
(7) |
|
|
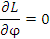 и, следовательно, второе уравнение Лагранжа
и, следовательно, второе уравнение Лагранжа