Пример 1. Лагранжиан свободной материальной точки в прямоугольной декартовой системе координат имеет вид
| |
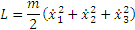 , ,
|
(1) |
|
где 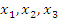 - координаты точки. - координаты точки.
Очевидно, что
| |
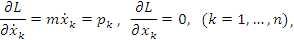
|
(2) |
|
где pk - компоненты импульса частицы.
Тогда из уравнений Лагранжа следует, что
pk = const и, следовательно, экстремалями являются прямые линии.
Пример 2. Лагранжиан частицы, движущейся в потенциальном поле, равен
| |
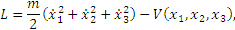
|
(3) |
|
где V (x1, x2, x3) - потенциальная
энергия частицы.
В этом случае уравнения Лагранжа представляют собой систему уравнений
| |
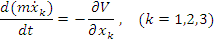 . .
|
(4) |
|
Произведение массы m частицы на компоненту ее скорости 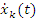 есть соответствующая компонента импульса pk частицы, а градиент потенциальной энергии системы,
взятый со знаком минус, равен силе, действующей на частицу. Поэтому уравнения (4) представляют собой координатную форму записи
векторного уравнения движения Ньютона:
есть соответствующая компонента импульса pk частицы, а градиент потенциальной энергии системы,
взятый со знаком минус, равен силе, действующей на частицу. Поэтому уравнения (4) представляют собой координатную форму записи
векторного уравнения движения Ньютона:
| |
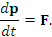
|
(5) |
|
|
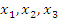 - координаты точки.
- координаты точки.
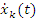 есть соответствующая компонента импульса pk частицы, а градиент потенциальной энергии системы,
взятый со знаком минус, равен силе, действующей на частицу. Поэтому уравнения (4) представляют собой координатную форму записи
векторного уравнения движения Ньютона:
есть соответствующая компонента импульса pk частицы, а градиент потенциальной энергии системы,
взятый со знаком минус, равен силе, действующей на частицу. Поэтому уравнения (4) представляют собой координатную форму записи
векторного уравнения движения Ньютона: