|
|
| Теорема Нётер |
|
|
|
|
|
В Теоремах 1 и 2 рассматривались функционалы инвариантные относительно специального семейства преобразований. Для общего семейства преобразований известен следующий результат. Теорема. Пусть семейство преобразований (
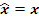 , а функции , а функции 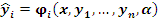 непрерывно дифференцируемы по непрерывно дифференцируемы по 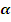 . Тогда, если функционал . Тогда, если функционал
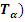 , то первым интегралом его системы уравнений Эйлера является , то первым интегралом его системы уравнений Эйлера является
Доказательство. Исходя из инвариантности функционала (2), имеем
Учитывая, что функция
Найдем
Поэтому (4) принимает вид
при Отсюда следует, что
Теорема доказана. |
|
|